데이터프레임 이용해서 패널 데이터 만들기

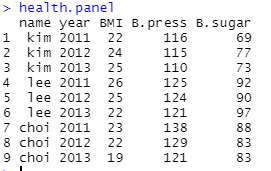
*함수를 이용하는 방법 : pdata.frame() 함수_plm패키지
3개의 데이터프레임을 rbind() 함수로 묶어 하나의 데이터 프레임으로 다시 생성하는 방법도 있음


pdata.frame(x,index,row.names)인데 row.names는 생성된 패널 자료의 행 이름을 출력할 것인지 결정, 기본값은 T
실행중인 패키지 종료 detach()
ARCH-GARCH 분석을 위한 패키지 : rugarch
시계열 자료 분석을 위한 패키지 : tseries, fGarch
일반적인 시계열 자료에는 오차항에 이분산이 존재하며, 분산의 변동이 군집 현상을 이루는 경향을 보인다. 이렇게 시간에 가변적으로 변하는 변동성을 측정하기 위해 고안된 모형이 자기회귀 조건부 이분산(ARCH)이며, 더 발전된 형태의 모형인 일반화된 자기회귀 조건부 이분산(GARCH)가 있다.
[단위근 검정]
단위근(Unit root)이 존재하는 불안정 시계열 간의 관계를 알아보기 위해 전통적인 방법을 이용해 회귀분석을 수행하는 경우 R2가 높아지는 가성적 회귀현상으로 인해 시계열 간에 보다 더 유의미한 관계가 존재하는 것 같은 비롯한 여러가지 문제가 발생하게 된다. 이런 경우 불안정 시계열을 일차 차분한 변수를 이용해 회귀분석을 수행함으로써 전통적 방법의 사용으로 인해 발생하게 되는 문제점들을 어느정도 해결할 수는 있지만 단순히 차분변수를 이용하여 회귀분석을 수행하게 되면 시계열들 사이의 장기적 관계에 대한 중요한 정보를 상실하게 된다. 엥글과 그랜저(Engle and Granger, 1987)에 의하면 불안정 시계열들 사이에 공적분 관계(cointegration)가 존재하는 경우 오차수정모형(VECM)모형을 사용함으로써 시게열 간의 장기적 관계에 대한 정보 상실을 회피할 수 있다. 따라서 경제변수들의 관계분석에서 불안정 시계열 간에 공적분이 존재하는지를 판단하는 과정은 중요한 의미를 가진다.
일반적으로 사용되는 공적분 검정법은 ADF의 단위근 검정 아이디어를 이용한 엥글과 그랜저(Engle and Granger, 1987)의 2단계 검정법과 ADF의 단위근 검정을 다변량의 경우로 확장하여 최우추정을 통한 검정을 수행하는 요한슨(Johansen, 1988, 1991)의 검정법 등을 들 수 있고, 일반적으로는 요한슨의 검정법이 보다 더 사용된다.
>> 요한슨의 공적분 검정, 오차수정모형(VECM)분석을 위한 패키지 : urca
1. 안정성 검정
두 시계열 변수가 모두 단위근을 갖는 불안정 시계열 변수라면 가성적 회귀현상과 같은 문제들이 발생하게 되므로, 먼저 두 시계열 변수가 안정적인지 여부를 확인해야 한다. 가장 일반적으로 사용되는 단위근 검정 방법인 확장된DF(ADF) 검정은 urca 패키지의 ur.df()함수로 수행할 수 있다.

type : 회귀식의 형태를 결정한다.
- "draft" 회귀식에 절편 항 추가
- "trend" 절편 항과 추세 항 추가
- "none" 회귀식에 아무것도 추가하지 않음
selectlags : 정보 기준(AIC, BIC)에 의해 시차를 결정한다.
- 생략 -
Value of test-statisitc is : -2.3396
| 1pct | 5pct | 10pct | |
| tau3 | -3.99 | -3.43 | -3.13 |
두 변수에 대한 ADF 검정통계량은 -2.3396과 -2.5159로 1% 유의수준의 임계값인 -3.99보다 크므로 단위근이 존재한다는 귀무가설이 기각되지 않는다. 따라서 두 변수 모두 단위근이 존재하는 불안정적 시계열임을 알 수 있으며, 이 경우 추가로 공적분 검정이 요구된다.
*안정적인 시계열이란?
어던 시계열의 평균이 시점 t에 대해 일정하고, 공분산은 t+k와 t에 의존하지 않고 단순히 시차인 k에만 의존한다면 시계열이 안정적이라고 한다. 확률행보(random walk) 과정을 따르는 시계열은 불안정적이며 이는 d차 차분 과정을 통해 안정적이 된다.
++ tseries 패키지를 이용한 ADF 검정
adf.test(x, alternative, k)
- alternative는 대립가설을 문자열로 나타낸다. 기본값은 안정적 (입력할 필요 x)
- k는 시차, 기본값은 계산된다.
예시) p-value가 0.99로 1에 가까워 5%수준에서 단위근이 존재한다는 귀무가설이 기각될 수 없다. 즉, 해당 시계열 변수는 불안정적이다.
2. 공적분 검정
공적분 검정 과정에서 일반적으로 사용되는 요한슨의 검정을 수행하기 위해 urca 패키지의 ca.jo()를 사용할 수 있다.

type : 통계량 추정 방법을 결정한다.
- "eigen" 최대고유치 통계량
- "trace" 트레이스 통계량
ecdet
- "none" 절편계수를 제외한다
- "const" 회귀식에 상수항을 추가한다
- "trend" 회귀식에 추세변수를 추가한다
spec : 모형의 구조에 따라 "longrun" 또는 "transitory"를 입력할 수 있다.
k : 시차를 입력한다. 기본값은 2
Values of teststatistic and critical values of test :
test .............. 1pct
r <= 1 | 5.86 16.26
r = 0 | 30.86 30.45
H0 : 공적분 벡터가 존재하지 않는다 (r=0) 하에서 계산된 검정통계량 30.86이 1% 유의수준의 임계값 30.45보다 크므로 귀무가설은 기각된다.H0 : 공적분 벡터가 하나 이하 존재한다 (r<=1) 하에서 계산된 검정통계량 5.86이 1% 유의수준 임계값 16.26보다 작으므로 귀무가설은 기각되지 않는다.따라서 두 변수 사이에는 안정적인 선형 결합, 즉 공적분 관계가 존재한다고 결론지을 수 있다.
++ 엥글과 그랜저 검정방법따로 함수를 제공하지 않기 때문에, 회귀모형을 추정한 후 얻게 되는 잔차항에 대해 단위근 검정 수행>> m1.res <- lm(M1~GDP, data = data)>> m1.resid <- resid(m1.res)>> adf.test(m1.resid)단위근이 존재한다는 귀무가설이 기각될 수 없는 경우, 두 변수는 공적분되어있지 않다.
3. VECM 분석
불안정 변수사이에 공적분 관계가 존재하는 경우 오차수정모형(VECM)을 사용할 수 있다. 함수는 cajools()를 사용한다.
#벡터오차수정모형(VECM) 분석을 위한 R 함수 : cajools(z, reg.number)
여기서 reg.number는 VECM 모형 내에서 몇 개의 방정식을 추가할 것인지 결정. 아무것도 입력하지 않으면 모든 방정식이 추정된다.
++ tsDyn 패키지의 VECM(data, lag, r, include, estim) 함수를 사용하는 방법도 있음
r : 변수 사이에 몇 개의 공적분 관계가 있는지 입력, 기본값은 1
include
- "none" 상수항과 추세항 제거
- "const" 회귀식에 상수항을 추가한다
- "trend" 회귀식에 추세변수를 추가한다
- "both" 모두 포함
estim
- "2OLS" 엥글그랜저 2단계 최소제곱추정량
- "ML" 요한슨 최우추정량
>>VECM.res <- VECM(data, lag=2, include="const", estim="2OLS")
4. VAR 분석
#벡터자기회귀(VAR) 분석을 위한 R 함수 : VAR(y, p, type, exogen, ic, lag.max)
패키지 - vars
p : 시차를 입력한다. 기본값은 1type
- "none" 모두 생략
- "const" 상수항 추가(기본값)
- "trend" 추세항 추가
- "both" 상수항, 추세항 모두 추가
ic : p인수에 시차를 직접 입력하지 않고 정보 기준에 의해 시차를 결정하고자 하는 경우. AIC가 기본값, 그 외 HQ, SC, FPE
lag.max : ic인수의 정보기준에 의해 시차를 결정할 경우 제한될 최대 시차
- 생략 -
Estimatoin results for equation prod(노동생산성) :
prod = prod.ㄱ1 + rw.ㄱ1
- 생략 -
rw.ㄱ1(실질임금)의 estimate는 0.008432, 실질임금의 시차변수 1 단위 증가는 노동생산성을 약 0.0084 증가시킨다.
*다중공선성 VIF 계산을 위한 R 함수 : vif(), HH 패키지
>>install.packages("HH")
*시계열 모형
AR모형 : P시점 전의 자료가 현재 자료에 영향을 주는 자기회귀모형
MA모형 : 유한한 개수의 백색잡음의 결합으로 언제나 정상성을 만족
MA1모형 : 시계열이 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합으로 이뤄진 모형
MA2모형 : 바로 전 시점의 백색잡음과 시차가 2인 백색잡음의 결합으로 이뤄진 모형
ARIMA 모형은 비정상시계열 모형으로, 차분과 변환을 통해 AR모형, MA모형, ARMA모형으로 정상화한다.
[Q통계량]
더빈-왓슨(DW)의 d통계량이나 h통계량을 이용해 시계열 자료나 잔차항에 1차 자기상관이 존재하는지를 검정할 수 있었다. 그러나 1차 자기상관이 존재하지 않아도, 2차, 3차 혹은 k차 자기상관이 존재할 수 있기 때문에 모든 차수에 대한 자기상관이 존재하는지를 검정해봄으로써 시계열 자료나 잔차항에 자기상관이 존재하는지를 보다 명확하게 판단할 수 있다. 따라서 복스와 피어스(Box and Pierce, 1970)는 다음 Q통계량을 제안한다.
#Q통계량 계산을 위한 R 함수 : Box.test(x, lag, type)
- type은 "Box-Pierce"와 "Ljung-Box"를 선택하여 입력
#시계열 자료로 변환
kospi.ts <- ts(kospi, start=c(1999,12), frequency=12)
ARCH 모형
ARCH 모형은 변수들의 집합의 실제값들의 조건하에 확률 오차항의 분포를 특징짓는다. ARCH 모형을 OLS로 추정하게 되면 ARCH 효과로 자기상관이 발생하게 되고 더빈-왓슨 통계량이 유의하게 나온다. 따라서 ARCH효과를 검정하기 위해 ARCH효과가 존재하지 않는다는 귀무가설을 설정하고, 다음과 같이 ARCH LM검정통계량을 계산할 수 있다.
#ARCH LM 검정을 위한 R 함수 : ArchTest() 함수 FinTS 패키지
GARCH 모형
GARCH모형은 ARCH모형의 조건부 분산함수의 시차 p가 길어지면서 생기는 불편함을 작은 모수를 추정하여도 지속적 변동성을 충분히 고려할 수 있는 일반화된 자기회귀 조건부 이분산 모형이다. GARCH모형 에서는 오차항의 조건부 분산이 시차오차에 의존할 뿐만 아니라 과거의 조건부 분산에 의존한다.#(G)ARCH모형 추정을 위한 R함수 : ugarchfit() 함수 rugarch 패키지#GARCH모형 설정을 위한 R함수 : ugarchspec()
'20대 성장기 > 공부' 카테고리의 다른 글
| 빅데이터 디자인실무 1급 과정_파이썬 프로그래밍 [5] 데이터 시각화 (0) | 2021.11.25 |
|---|---|
| 빅데이터 디자인실무 1급 과정_파이썬 프로그래밍 [4-3] 판다스 기본문법 (0) | 2021.11.25 |
| 빅데이터 디자인실무 1급 과정_파이썬 프로그래밍 [4-2] 웹크롤링 (0) | 2021.11.24 |
| 빅데이터 디자인실무 1급 과정_파이썬 프로그래밍 [4] 웹크롤링 (0) | 2021.11.23 |
| 빅데이터 디자인실무 1급 과정_파이썬 프로그래밍 [3-2] 코드 정리 (0) | 2021.11.23 |