- 다중회귀분석의 기초

식에 경력(exper)이 명시적으로 포함되어 있으므로 경력을 고정할 때 교육이 임금에 미치는 영향을 측정할 수 있다. 단순회귀분석에서는 exper가 오차항에 들어가 있으며 이 때에는 경력이 교육과 상관되지 않았다고 가정해야만 한다. 연구 목적 상 흥미로운 계수는 β1, 즉 educ가 wage에 미치는 ceteris paribus효과이다. 모형에서는 exper을 명시적으로 모형에 포함시킴으로써 exper의 효과를 통제할 수 있게 된다.
β1 : 다른 요소를 통제한 이후 educ의 변화가 wage에 미치는 효과
β2 : 다른 요소를 통제한 이후 exper의 변화가 wage에 미치는 효과
다중회귀분석은 종속변수와 독립변수 간의 관계가 선형이 아닌 경우에도 유용하다. 예를 들어 가구 소비(cons)가 가구소득(inc)의 2차함수라고 가정하는 경우 두 개의 독립변수가 있는 회귀모형으로 손쉽게 쓸 수 있다.

다만 모수들을 해석할 때, 한계소비성향은
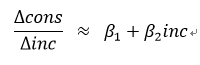
이므로, 소득이 소비에 주는 한계효과는 β1뿐 아니라 β2와 소득 수준 자체에 의존한다.

β1 : 다른 조건이 일정할 때 salary의 sales에 대한 탄력성
β3 = 0 : 100β2는 ceoten이 1년 증가할 때 salary의 ceteris paribus 백분율 증가를 대략적으로 나타난다.
여러 개의 변수가 동시에 달라질 때의 효과를 알고 싶은 경우, 예를 들면 어떤 사람이 추가적인 교육 없이 현재의 직장에서 1년 더 일할 경우 임금의 상승도를 예측하고자 할 때, exper와 tenure가 모두 1년씩 증가하므로, exper와 tenure의 계수를 합산한 2.6%이다.

회귀에 독립변수가 추가되면 R제곱은 아주 조금이라도 증가한다.
- 다중공선성
다중공선성(Multicollinearity) : 두 개 이상의 독립변수들 간에 존재하는 고도한 상관관계. 다중공선성이 높아지면 회귀계수의 표준오차가 비정상적으로 커진다. 회귀계수의 유의성은 t값에 의해 결정되는데, t값은 회귀계수 β/표준오치로 계산되기 때문에 t 값이 작아져서 유의해야할 변수가 유의하지 않게 된다.
- 상관계수가 만약 0.9를 넘는다면 다중공선성의 문제가 있을 수 있음
- R제곱이 1이라면 독립변수 간 심각한 상관관계가 있음을 의미
- 분산팽창지수(VIF:Variance Inflation Factor) = 1/(1-R제곱) 이 크다는 것은 다중공선성이 크다는 의미
- 일반적으로 10보다 크면 문제가 있다고 판단
- 더미변수의 경우 VIF가 3이상이라면 다중공선성을 의심할 수 있음
다중공선성이 있음에도 불구하고 해당 독립변수가 유의하다면, 표준오차가 비정상적으로 팽창되었음에도 유의하다는 의미이므로 그대로 두어도 무방하다. 특히 조절효과를 확인하기 위해 교호작용(interaction)변수를 추가하는 경우 연구자가 의도적으로 넣음으로써 어느 정도의 다중공선성을 피할 수 없다. 따라서 약간의 다중공선성의 문제가 발생하더라도 연구자의 의도와 변수의 유의성에 따라 결정해야 한다. 중요변수가 아닌 경우 해당 변수를 제거함으로 다중공선성 문제를 제거한다. 평균을 이용해 다중공선성이 높은 변수들을 합치는 방법도 존재한다.

'20대 성장기 > 공부' 카테고리의 다른 글
| 계량경제학 5. 질적인 정보와 다중회귀분석 (0) | 2021.05.11 |
|---|---|
| 계량경제학 4. 다중회귀분석_추론 (0) | 2021.05.11 |
| 계량경제학 2. 단순회귀모형 (0) | 2021.05.10 |
| 계량경제학 1. 계량경제학과 경제 자료의 속성 (0) | 2021.05.10 |
| 논문 작성을 위한 통계 읽기 (0) | 2021.04.23 |